Exercice : TD1 - Statique des fluides [Dr (HDR) Sylvain Serra]

TD1 - Statique des fluides

Exercice 1

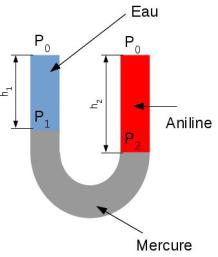
Au fond d'un tube en U, on verse du mercure. on verse de l'eau dans l'une des branches et de l'aniline dans l'autre, de telle sorte que les surfaces libres soient dans un même plan horizontal.

L'eau occupe alors une hauteur \(h_1\) et l'aniline une hauteur \(h_2\)

Question

Quelle est la masse volumique de l'aniline \(\rho_a\) ?

Données :

masse volumique du mercure \(\rho_{Hg} = 13.6\ kg\ dm^{-3}\)
\(h_1 = 20\ cm\)
\(h_2 = 22.2 \ cm\)

Indice

eau : \( P_1 = P_0+\rho_e g h_1\)

aniline : \( P_2 = P_0+\rho_a g h_2\)

mercure : \(P_2-P_1 = \rho_{Hg}g (h_2-h_1)\)

Indice

\(P_2-P_1 = \rho_a g h_2 -\rho_e g h_1 = \rho_{Hg} g (h_2-h_1)\)

\(\rho_a = \frac{\rho_{Hg} g (h_2-h_1) + \rho_e g h_1}{gh_2}\)

Exercice 2

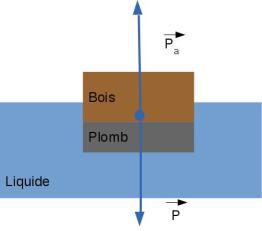
Un bloc de bois de masse est lesté par un bloc de plomb.

Question

Calculer le poids du bloc de plomb pour que le solide flotte sur un liquide de densité \(d_l\) et que \(\frac{4}{5}\) de son volume soient immergés.

Données :

densité du bois \(d_b = 0.6\)
masse du bloc de bois \(m_b = 180 \ g\)
densité du plomb \(d_{pb} = 11.3\)
densité du liquide \(d_l = 0.9\)

Indice

Équilibre : \(\vec{P}+\vec{P_a}=0 \Leftrightarrow P=P_a\)

Indice

\(P_b+P_{Pb}=P_a=\frac{4}{5}\rho_lVg\)

\(m_bg+P_{Pb} = \frac{4}{5}\rho_ed_l(V_b+V_{Pb})g\)

avec \(V_b=\frac{m_b}{\rho_e d_b}\) et \(V_{Pb}=\frac{m_{Pb}}{\rho_e d_{Pb}}\)

\(m_b g+P_{Pb}=\frac{4}{5} g\frac{m_b}{d_b}d_l+\frac{4}{5}\frac{P_{Pb}}{d_{Pb}}d_l\)

Indice

\(P_{Pb}=\frac{gm_b\left(\frac{4d_l}{5d_b}-1 \right)}{1-\frac{4d_l}{5d_{Pb}}}\)

Exercice 3

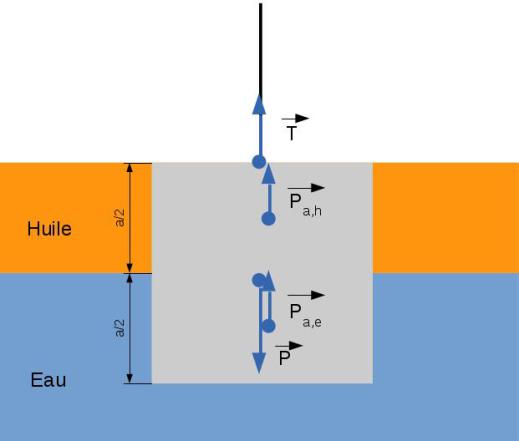
Un cube d'aluminium de côté \(a\) est suspendu à une corde. Le cube est immergé à moitié dans l'huile et à moitié dans l'eau.

Question

Calculer la tension de la corde

Données :

\(a = 15\ cm\)
densité de l'huile \(d_h= 0.8\)
densité de l'aluminium \(d_{Al} = 2.64\)

Indice

Équilibre : \(\vec{T} + \vec{P}+\overrightarrow{P_{a,e}}+\overrightarrow{P_{a,h}} = 0\)

Indice

\(\rho_{Al}Vg=T+\rho_e\frac{V}{2}g+\rho_h\frac{V}{2}g\)

\(T=Vg\left(-\frac{1}{2} (\rho_e+\rho_h)+\rho_{Al}\right)\) avec \(V=a^3\)

Exercice 4

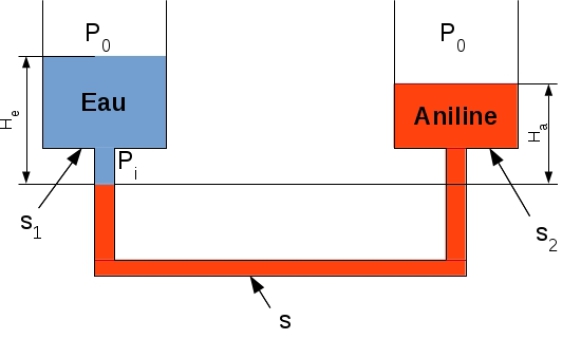
Un manomètre différentiel est formé de deux cylindres de sections droites respectives \(S_1\) et \(S_2\), reliés par un tube de section intérieure \(s\) constante.

L'ensemble contient deux liquides incompressibles non miscibles entre eux : l'eau de masse volumique \(\rho_e\) et l'aniline de masse volumique \(\rho_a\). Initialement la pression au dessus des deux liquides est la même (pression atmosphérique\( P_0\)). On provoque au dessus de l'eau du récipient de gauche une surpression \(\Delta P\).

Question

Déterminer le déplacement \(\Delta h\) de la surface de séparation entre l'eau et l'aniline dans le tube.

On négligera tout phénomène lié à la tension superficielle au niveau des interface entre les différents fluides.

Évaluer la sensibilité \(\frac{\Delta h}{\Delta P}\) du manomètre. Commenter le résultats.

Données :

Masse volumique de l'aniline \(\rho_a = 1.024\ g\ cm^{-3}\)
Masse volumique de l'eau \(\rho_e = 0.998\ g\ cm^{-3}\)
\(S_1=S_2=100 \times s\)

Indice

A l'équilibre :

\(P_i\) = pression à l'interface eau-aniline

\(P_i = P_0+\rho_e g H_e = P_0+ \rho_agH_a\)

\(\rho_eHe=\rho_aHa\) (1)

Indice

Surpression \(\Delta P\) sur le réservoir de gauche rempli d'eau

\(\Rightarrow\) nouvelle interface \(\Rightarrow\) déplacement de \(\Delta h\)

Indice

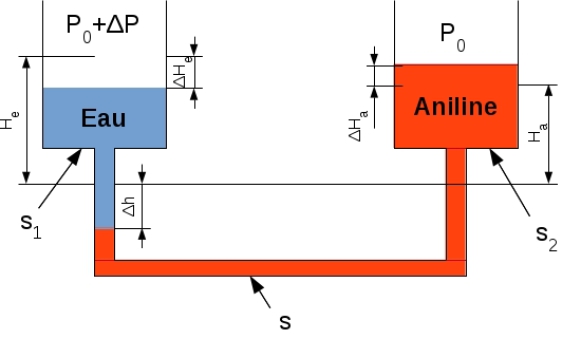
\(P_i = (P_0+\Delta P) +\rho_e g(H_e-\Delta H_e+\Delta h)\) (2)

Indice

On a conservation du volume d'eau donc :

\(\Delta He S_1=\Delta h s\)

\(\Delta H_e = \frac{\Delta hs}{S_1}\)

Indice

De même pour l'aniline :

\(\Delta H_a = \frac{\Delta hs}{S_2}\)

et \(P_i = P_0 +\rho_a g(H_a+\Delta H_a+\Delta h)\) (3)

Indice

(2) et (3) puis (3) \(\Rightarrow\) \((\cancel{P_0}+\Delta P) +\rho_e g\left(\cancel{H_e}+\Delta h\left(1-\frac{s}{S_1}\right)\right) = \cancel{P_0} +\rho_a g\left(\cancel{H_a}+\Delta h\left( 1+\frac{s}{S_2}\right)\right)\)

\(\Rightarrow\) \(\Delta P +\rho_e g\Delta h\left(1-\frac{s}{S_1}\right) = \rho_a g\Delta h\left( 1+\frac{s}{S_2}\right)\)

\(\Rightarrow\) \(\Delta h = \frac{\Delta P}{\rho_a g\left( 1+\frac{s}{S_2}\right)-\rho_e g\left(1-\frac{s}{S_1}\right)}\)

Solution

A.N. \(\frac{\Delta h}{\Delta P} = 2.2\ 10^{-3} \ m\ Pa^{-1}\ \Rightarrow \) Manomètre très sensible

Exercice 5

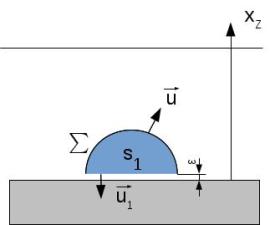
Un solide hémisphérique de rayon R repose sur le fond d'un récipient contenant un fluide incompressible de masse volumique \(\rho\). La surface libre du fluide est à une hauteur \(h\) par rapport au fond horizontal. La pression à l'air libre et la pression au fond du récipient sont respectivement notées \(P_0\) et \(P_1\).

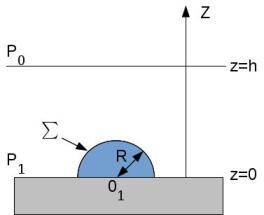
Question

Déterminer par un calcul direct, la résultante des forces de pression sur la surface \(\Sigma\) du solide en contact avec le fluide.

Quelle remarque vous inspire l'expression obtenue ?

Donner un autre méthode de calcul, plus rapide, permettant d'obtenir ce résultat.

Indice

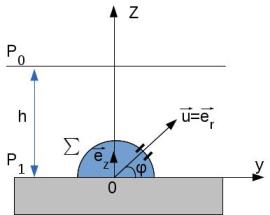
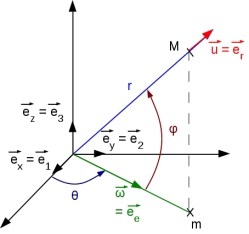
\(x=r\ cos \varphi\ cos \theta\)

\(y=r\ cos\varphi\ sin \theta\)

\(z = r\ sin\varphi\)

Indice

Résultantes des forces de pression :

\(\overrightarrow{F} = \displaystyle \iint_\Sigma \overrightarrow{dF}=\iint_\Sigma \overrightarrow \sigma dS =\iint_\Sigma -PdS\vec{u}\)

avec \(\vec{u} = cos\varphi\ \vec{\omega} + sin \varphi\ \overrightarrow{e_z} = \overrightarrow{e_r}\) et \(\vec{\omega} = cos\theta\ \overrightarrow{e_x}+sin\theta\ \overrightarrow{e_y} = \overrightarrow{e_e}\)

Indice

d'après la loi de l'hydrostatique entre \(A\) et \(M\)

\(P_A+\rho g x_3^{A}=P_M+\rho g x_3^{M}\)

\(P_0+\rho g h=P_M+\rho g x_3\)

\(P_M=P =P_0+\rho g (h-x_3)\)

Indice

l'expression de \(dS\) est donnée par le paramétrage de \(\Sigma\).

On a :

\(\Sigma=\left\{ (x_1,x_2,x_3-\in \mathbb{R}^3 \right\}\ \ \ x_1=R\cos \varphi\cos \theta ; x_2=R\cos\varphi\sin \theta; x_3 = R\sin\varphi\ \ \ (\theta, \varphi)\in[0 ;2\pi]x[0 ;\pi/2]\)

donc :

\(\gamma :\left\{ \begin{array}{l}x_1=R\cos\varphi \cos\theta=\gamma_1(\varphi,\theta)\\ x_2=R\cos\varphi \sin\theta=\gamma_2(\varphi,\theta)\\ x_3=R\sin \varphi=\gamma_3(\varphi , \theta)\end{array} \right.\)

Indice

\(\frac{\partial\gamma}{\partial\theta}= \hspace{3cm }\frac{\partial\gamma}{\partial\varphi}= \)

Indice

\(\frac{\partial\gamma}{\partial\theta}= \left( \begin{array}{l}-R\cos\varphi \sin \theta\\R\cos \varphi\cos\theta\\0\end{array}\right) \ \ \ \ \frac{\partial\gamma}{\partial\varphi}= \left( \begin{array}{l}-R\sin\varphi \cos \theta\\-R\sin \varphi\sin\theta\\R\cos\varphi\end{array}\right)\)

Indice

\(\frac{\partial\gamma}{\partial\theta} \wedge \frac{\partial\gamma}{\partial\varphi}= \)

Indice

\(\frac{\partial\gamma}{\partial\theta} \wedge \frac{\partial\gamma}{\partial\varphi}= \left( \begin{array}{l}R^2\cos^2\varphi \cos \theta\\R^2\cos^2 \varphi\sin\theta\\R^2\cos\varphi\sin\varphi\sin^2\theta+R^2\cos\varphi\sin\varphi\cos^2\theta=R^2\cos\varphi\sin\varphi\end{array}\right)\)

Indice

\(\left\| \frac{\partial\gamma}{\partial\theta} \wedge \frac{\partial\gamma}{\partial\varphi}\right\|=\)

Indice

\( \left\| \frac{\partial\gamma}{\partial\theta} \wedge \frac{\partial\gamma}{\partial\varphi}\right\|=\sqrt{R^4\cos^4\varphi+R^4\cos^2\varphi\sin^2\varphi}=R^2\cos\varphi\)

donc \( dS=\left\| \frac{\partial\gamma}{\partial\theta} \wedge \frac{\partial\gamma}{\partial\varphi}\right\|d\theta d\varphi=R^2\cos\varphi d\theta d\varphi\)

Indice

\(\overrightarrow{F} = \displaystyle \int_0^{2\pi} \int_0^{\pi/2} -P\underbrace{\vec e_r}_{\vec{u}} \underbrace{R^2\cos\varphi d\theta d\varphi}_{dS} =\)

Indice

\(\overrightarrow{F} = \displaystyle \int_0^{2\pi} \int_0^{\pi/2} -\left[P_0+\rho g (h-R \sin\varphi)\right]\left(R^2\cos^2\varphi\cos\theta \vec e_1+R^2\cos^2\varphi\sin\theta \vec e_2+R^2\cos\varphi\sin\varphi \vec e_3 \right)d\theta d\varphi\)

Indice

\(\overrightarrow{F} = \vec e_1 \displaystyle \int_0^{2\pi} \int_0^{\pi/2} R^2\cos\theta d\theta...+\vec e_2 \displaystyle \int_0^{\pi/2} \int_0^{2\pi} \sin\theta d\theta... +\vec e_3 \displaystyle \int_0^{2\pi} \int_0^{\pi/2}-\left[P_0+\rho g (h-R \sin\varphi)\right]R^2\cos\varphi\sin\varphi d\theta d\varphi \)

Indice

\(\overrightarrow{F} = \vec e_3 2\pi \displaystyle \left[ \int_0^{\pi/2}-(P_0+\rho g h)R^2\cos\varphi\sin\varphi d\varphi+ \int_0^{\pi/2}\rho g R^3\cos\varphi\sin^2\varphi d\varphi\right] \)

\(= \vec e_3 2\pi \left[ -(P_0+\rho g h)R^2\left[ \displaystyle\frac{1}{2}\sin^2\varphi\right]^{\pi/2}_0+\rho g R^3 \left[ \displaystyle\frac{1}{3}\sin^3\varphi\right]^{\pi/2}_0\right]\) aide de math

Indice

\(\overrightarrow{F} =\left( \rho g \displaystyle\frac{2}{3} \pi R^3-(P_0+\rho g h )\pi R^2\right)\vec e_3\)

Indice

Solution

\(\displaystyle \overrightarrow{P_A}=\iint_{(\Sigma + S_1)}-P\vec{u}dS=\iint_\Sigma -P\vec{u}dS+\iint_{s_1}-P\overrightarrow{u_1} ds\)

\(\displaystyle \overrightarrow{P_A}=\overrightarrow{F}-\iint_{s_1}P_1\overrightarrow{u_1} ds\)

\(\frac{2}{3} \pi R^3 \rho g \overrightarrow{e_z}=\overrightarrow{F}-P_1S_1\overrightarrow{u_1}=\overrightarrow{F}+P_1S_1\overrightarrow{e_z}\)

\(\overrightarrow{F}=\left( \frac{2}{3} \pi R^3 \rho g -P_1\pi R^2\right)\overrightarrow{e_z}=\left[\rho g \frac{2}{3}\pi R^3-(P_0+\rho g h)\pi R^2\right] \overrightarrow{e_z}\)

Exercice 6

La température est la pression étant respectivement \(T_0=0\ °C\) et \(P_0=1\ bar\) au niveau de la mer \((x_3=0)\).

Question

Calculer la pression au sommet de l'Everest \((8880\ m)\) dans l'hypothèse \(T=Cte\).

Indice

\(T= cte\), masse gazeuse isotherme

\(\rho \vec{g}-\nabla P = 0 \Rightarrow \left\{ \begin{array}{l}\displaystyle \frac{\partial P}{\partial x_1}=0 \\ \frac{\partial P}{\partial x_2}=0 \\ \frac{\partial P}{\partial x_3}=-\rho g \end{array} \right.\)

Indice

\(\frac{d P}{d x_3}=-\rho g\)

\(dP=-\rho(x_3) g dx_3\)

Indice

\(PV = nRT \Rightarrow \frac P \rho = rT\) avec \(\frac RM = r\)

\(dP=-\frac{P}{rT}gdx_3\)

Indice

\(\frac{dP}{P}=-\frac{1}{rT}gdx_3\)

Indice

\(\ln \frac{P}{P_0}=-\frac{1}{rT}gx_3\)

Solution

\(P = P_0 e^{-\frac{\rho_0g}{P_0}\displaystyle x_3}\)

AN : \(P = 3.28 \ 10^4\ Pa\)

Méthode :

\(T_0 = 273\ K\)

\(\rho_0 = \frac{P_0}{rT_0} = 1.28\ kg\ m^{-3}\)

\(r = \frac{8.31}{29\ 10^{-3}}\)

Question

Un modèle plus réaliste suppose que l'atmosphère est polytropique. Ce modèle conduit à une variation de la température linéaire avec l'altitude : \(T=T_0-ax\).

Sachant que \(a = 6.5\ K\ km^{-1}\), donner la valeur de la constante \(k\).

Calculer avec ce nouveau modèle la température et la pression au sommet de l'Everest.